The mathematics of sunflowers
On the road near Tahuna this field of sunflowers caught our eye. How could we not stop and snap?
Here’s something I never knew about these summer friends – a mathematical model for the pattern of florets has been devised by H Vogel. Thus:
where θ is the angle, r is the radius or distance from the center, and n is the index number of the floret and c is a constant scaling factor. It is a form of Fermat’s spiral. The angle 137.5° is related to the golden ratio (55/144 of a circular angle, where 55 and 144 are Fibonacci numbers) and gives a close packing of florets. Thank you Wikipedia!
(Does popping a small amount of maths into any writing instantly make it more impressive? Check out what Waikato University physicist Marcus Wilson has to say on the subject… )


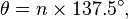




Pingback: Tauhei pikelets the best | Number 8 Network
Pingback: Tauhei pikelets simply the best - Number 8 Network